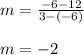Answer:
For the table on the left the rate of change is
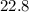
For the table on the left the rate of change is
Explanation:
The range of change is the slope. The slope can be found with the following formula:
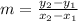
For the table on the left
Choose two points. In this case you can choose (-1,-24), (4,90)
You can say that:
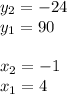
Substituting these values into the formula, you get:
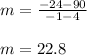
For the table on the right
Choose two points. You can choose (3,-6), (-6,12)
You can identify that:
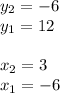
Substituting these values into the formula, you get: