Question

70% of voters in a certain state support an increase in the minimum wage. A researcher believe that the percentage of fast food workers for support and increase is higher than 70%. In a random sample of 300 fast food workers for 240 supporters increase an minimum-wage. Test is significant level a = .05 find

Answer 1

Answer with explanation:

Let p be the proportion of voters in a certain state support an increase in the minimum wage.

As per given , we have

`H_0: p =0.70\\\\ H_a: p >0.70`

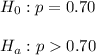
Since alternative hypothesis is right-tailed so the test is a right-tailed test.

Test statistic :
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

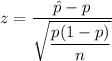
, where n= sample size.

p= population proportion.

`\hat{p}` = sample proportion.

. In a random sample of 300 fast food workers for 240 supporters increase an minimum-wage.

i.e. n= 300 and
`\hat{p}=(240)/(300)=0.8`

Then,

`z=\frac{0.8-0.7}{\sqrt{(0.7(1-0.7))/(300)}}\approx3.78`

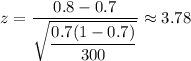
For significant level α = .05 , the critical z-value is

`z_(0.05)=1.645`

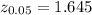
Decision : Since calculated z-value (3.78) is greater than the critical value (1.645) , so we reject the null hypothesis.

Conclusion : We have sufficient evidence o support researcher's claim that that the percentage of fast food workers for support and increase is higher than 70%..