Question

A rectangle is 13 centimeters wide and 18 centimeters long. how long is it’s diagonal

Answer 1

The length of the diagonal = 22.20 cm

Explanation:

Here, the length of the rectangle = 18 cm

Also, the width of the rectangle = 13 cm

Let us assume the diagonal of the rectangle = k cm

As we know, EACH INTERIOR ANGLE OF THE RECTANGLE = 90°

So, if we join the opposite vertices of the rectangle, a Right angled triangle is formed.

Here, the length of the Rectangle = Perpendicular of the right Δ

Width of the Rectangle = Base of the right Δ

Diagonal of the Rectangle = Hypotenuse of the right Δ

Now, by PYTHAGORAS THEOREM:

`(Base)^2 + (Perpendicular)^2  = ( Hypotenuse)^2`

or,
`(Width)^2 + (Length)^2  = ( Diagonal)^2`

`\implies (13)^2 + (18)^2  = (m)^2\\\implies 169 + 324= m^2\\\implies m^2 =  493\\\implies m = √(493)  = 22.20`

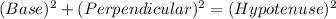
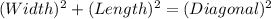
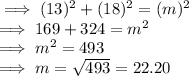
or, Diagonal = 22.20 cm

Hence, the length of the diagonal = 22.20 cm