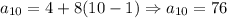Answer:
1)
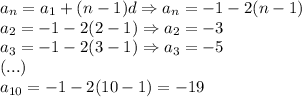
2)
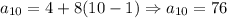
Explanation:
1) To write an Arithmetic Sequence, as an Explicit Term, is to write a general formula to find any term for this sequence following this pattern:

"Write an explicit formula for each explicit formula A(n)=-1+(n-1)(-2)"
This isn't quite clear. So, assuming you meant
Write an explicit formula for each term of this sequence A(n)=-1+(n-1)(-2)
As this A(n)=-1+(n-1)(-2) is already an Explicit Formula, since it is given the first term
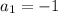 the common difference
the common difference
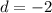 let's find some terms of this Sequence through this Explicit Formula:
let's find some terms of this Sequence through this Explicit Formula:
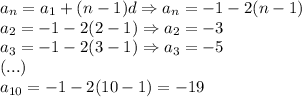
2)
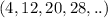 In this Arithmetic Sequence the common difference is 8, the first term value is 4.
In this Arithmetic Sequence the common difference is 8, the first term value is 4.
Then, just plug in the first term and the common difference into the explicit formula: