Question

In the diagram shown, parallelogram MNPQ is shown with points located on it's such that MU ≅ SP and RN ≅ QT.

Prove that RSTU must be a parallelogram.

Answer 1

See explanation

Explanation:

MNPQ is a parallelogram. Then

• 
  `MQ\cong NP;`
• 
  `MN\cong QP.`

By segment addition postulate,

• 
  `MQ\cong QU+UM;`
• 
  `PN\cong PS+SN;`
• 
  `QP\cong QT+TP;`
• 
  `MN\cong MR+RN.`

Given that MU ≅ SP and RN ≅ QT, then
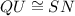`QU\cong SN` and
`MR\cong TP.`

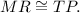
Consider triangles QUT and NSR. In these triangles,

• 
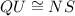  `QU\cong NS` - proven;
• 
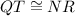  `QT\cong NR` - given;
• 
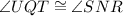  `\angle UQT\cong \angle SNR` - as opposite ngles of parallelogram MNPQ.

By SAS postulate, triangles QUT and NSR are congruent. Then
`UT\cong SR.`

Consider triangles MRU and PTS. In these triangles,

• 
  `MR\cong PT` - proven;
• 
  `MU\cong PS` - given;
• 
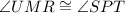  `\angle UMR\cong \angle SPT` - as opposite ngles of parallelogram MNPQ.

By SAS postulate, triangles MRU and TPS are congruent. Then
`UR\cong TS.`

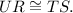
In quadrilateral RSTU,
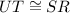`UT\cong SR` and
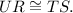`UR\cong TS.` Since opposite sides of the quadrilateral are congruent, the quadrilateral is a parallelogram.