Question

A ball is thrown upwards from the edge of a cliff. The horizontal velocity and vertical velocity are both 20m/s the distance from the ball to the bottom of the cliff is 100m/s. How high does the ball go? How long does it take the ball to hit the ground, from the time it leaves the child's hand?

Answer 1

20m

6.9s

Step-by-step explanation:

The vertical velocity of the ball is 20m/s. We can calculate the kinetic energy which gets transferred to potential energy once it gets to the top.

`E_k = E_p`

`0.5mv^2 = mgh`

`h = (0.5v^2)/(g)`

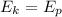
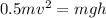
we can subtitute v = 20m/s and g = 10m/s2

`h = (0.5*20^2)/(10) = 20 m`

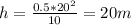
So the ball could go 20m high from the child hand, or 120m fro the bottom of the cliff.

The time it takes for the ball to travels to the top is the time it takes for it to decelerate from 20m/s to 0m/s with gravitational deceleration g = 10m/s2

t = v / g = 20 / 10 = 2s

Then the ball will start accelerating down ward with a constant acceleration of g = 10m/s. In order to cover distance d of 120m from the top to the bottom of the cliff

`d = (gt_2^2)/(2)`

`t^2 = (2d)/(g) = (2*120)/(10) = 24`

`t = √(24) = 4.9s`

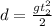
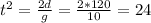
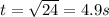
So the total time it takes is 4.9 + 2 = 6.9s