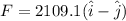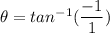Question

A 1200 kg car moving at 5.8 m/s is initially traveling north in the positive y direction. After completing a 90° right-hand turn to the positive x direction in 3.3 s, the inattentive operator drives into a tree, which stops the car in 270 ms. What is the magnitude of the impulse on the car; (a) due to the turn (b) due to the collision? What is the magnitude of the average force that acts on the car (c) during the turn and (d) during the collision? (e) What is the angle between the average force in (c) and the positive x direction?

Answer 1

given,

mass of car = 1200 Kg

initial velocity in north = 5.8 m/s

90° right-hand turn in time = 3.3 s

car stop in, time = 270 ms

a) impulse = change in momentum

Initial momentum = ( m x v) j

= ( 5.8 x 1200 ) j

= ( 6960) j

final momentum after turn is 90°

= 6960 i

impulse = 6960 i - 6960 j

impulse = 6960 ( i - j )

b) due to collision

initial momentum after turning = 6960 i

final momentum is equal to zero

impulse = 0 - 6960 i

impulse = - 6960 i

c) during turn

I = F Δ t

`F = (I)/(t)`

`F = \frac{6960 ( \hat{i} -\hat{j})}{3.3}`

`F =2109.1 ( \hat{i} -\hat{j})`

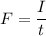
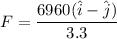
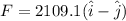
magnitude of force

`F =2109.1√(2)`

`F =2982.72\ N`

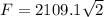
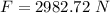
d) during collision

`F = (I)/(t)`

`F = \frac{-6960 \hat{i} }{0.27}`

`F =-25777.78\hat{i}\ N`

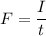
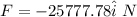
magnitude of average force is equal to

`F =25777.78\ N`

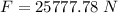
e) angle between average force

`F =2109.1 ( \hat{i} -\hat{j})`

`\theta =tan^(-1)((-1)/(1))`

`\theta =-45^0`