Question

Use sigma notation to represent the sum of the first six terms of the following sequence: −10, −13, −16, …

the summation from n equals one to 6 of quantity negative 10 plus 3 times n

the summation from n equals one to 6 of quantity negative 7 minus 10 times n

the summation from n equals one to 6 of quantity negative 7 minus 3 times n

the summation from n equals one to 6 of quantity negative 7 plus 3 times n

Answer 1

"the summation from n equals one to 6 of quantity negative 7 minus 3 times n"

Explanation:

General term of an arithmetic sequence:

`a_n=a_1+(n-1)r`

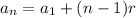
Where

`a_1` is the first term

n is the number of terms

r is the common difference

The value of r can be found by subtracting two consecutive values

`r=a_2-a_1=-13+10=-3`

Then

`a_n=-10+(n-1)(-3)=-7-3n`

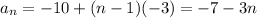
If we want to sum the first six terms of the sequence, we must find

`\sum_(n=1)^(n=6)(-7-3n)`

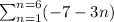
The correct option is

"the summation from n equals one to 6 of quantity negative 7 minus 3 times n"