Answer:
drawing ratio = 1.81176
reduction = 0.4480 = 44.80 %
drawing force is = 162724.682 lb
blank holder force = 95481.10 lb
Step-by-step explanation:
given data
cylindrical cup diameter = 4.25 in
cup height = 2.65 in
stock thickness = 3/16 in
blank diameter = 7.7 in
Punch and die radii = 5/32 in
so Punch diameter will be = 2 × 5/32 in = 0.3125 in
tensile strength = 65,000 lb/in²
yield strength = 32,000 lb/in²
shear strength of 40,000 lb/in²
to find out
(a) drawing ratio, (b) reduction, (c) drawing force, and (d) blankholder force
solution
first we get drawing ratio hat is express as
drawing ratio =
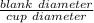 ..................1
..................1
put here value
drawing ratio =
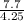
drawing ratio = 1.81176
and
reduction will be here
reduction =
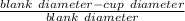 .................2
.................2
reduction =
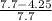
reduction = 0.4480 = 44.80 %
and
drawing force will be
drawing force is = k× π× cup diameter × stock thickness × tensile strength ........................3
here k = 1
so put here value
drawing force is = 1 × π× 4.25 ×
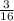 × 65000
× 65000
drawing force is = 162724.682 lb
and
blank holder force will be here as
blank holder force = maximum punch load ×
 ........................4
........................4
so here maximum punch load will be
maximum punch load = π × punch diameter × stock thickness × tensile strength × (
 - 0.7 ) .......................5
- 0.7 ) .......................5
here 0.7 is correction factor
maximum punch load = π × 0.3125 ×
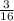 × 65000 × (
× 65000 × (
 - 0.7 )
- 0.7 )
maximum punch load = 286443.30 lb
so
blank holder force = 286443.30 ×

blank holder force = 95481.10 lb