Question

Samir is an expert marksman. When he takes aim at a particular target on the shooting range, there is a 0.950.950, point, 95 probability that he will hit it. One day, Samir decides to attempt to hit 101010 such targets in a row.

Answer 1

.401

Explanation:

However if it states to round to the nearest tenth then its .4

Answer 2

The question is incomplete. Here is the complete question:

Samir is an expert marksman. When he takes aim at a particular target on the shooting range, there is a 0.95 probability that he will hit it. One day, Samir decides to attempt to hit 10 such targets in a row.

Assuming that Samir is equally likely to hit each of the 10 targets, what is the probability that he will miss at least one of them?

Answer:

40.13%

Explanation:

Let 'A' be the event of not missing a target in 10 attempts.

Therefore, the complement of event 'A' is
`\overline A=\textrm{Missing a target at least once}`

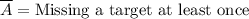
Now, Samir is equally likely to hit each of the 10 targets. Therefore, probability of hitting each target each time is same and equal to 0.95.

Now,
`P(A)=0.95^(10)=0.5987`

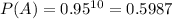
We know that the sum of probability of an event and its complement is 1.

So,
`P(A)+P(\overline A)=1\\\\P(\overline A)=1-P(A)\\\\P(\overline A)=1-0.5987\\\\P(\overline A)=0.4013=40.13\%`

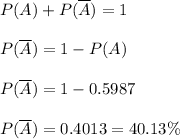
Therefore, the probability of missing a target at least once in 10 attempts is 40.13%.