Question

Scores on a certain intelligence test for children between ages 13 and 15 years are approximately normally distributed with μ=106 and σ=15. (a) What proportion of children aged 13 to 15 years old have scores on this test above 92 ? (Reminder: proportions are between 0 and 1 - don't put in percentages!)

Answer 1

Answer: 0.8238

Explanation:

Given : Scores on a certain intelligence test for children between ages 13 and 15 years are approximately normally distributed with
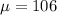`\mu=106` and
`\sigma=15`.

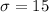Let x denotes the scores on a certain intelligence test for children between ages 13 and 15 years.

Then, the proportion of children aged 13 to 15 years old have scores on this test above 92 will be :-

`P(x>92)=1-P(x\leq92)\\\\=1-P((x-\mu)/(\sigma)\leq(92-106)/(15))\\\\=1-P(z\leq })\\\\=1-P(z\leq-0.93)=1-(1-P(z\leq0.93))\ \ [\because\ P(Z\leq -z)=1-P(Z\leq z)]\\\\=P(z\leq0.93)=0.8238\ \ [\text{By using z-value table.}]`

Hence, the proportion of children aged 13 to 15 years old have scores on this test above 92 = 0.8238