Question

A frictionless, incompressible steady flow field is given by V = 2xyi − y2j (2) in arbitrary units. Let the density be rhoo = constant and neglect gravity. Find expressions for the pressure gradients in both the x and y directions.

Answer 1

pressure gradient in x direction:

`(\partial p)/(\partial x) = -\rho 2xy^(2)`

pressure gradient in y direction:

`(\partial p)/(\partial y) = \rho 2y^(3)`

Step-by-step explanation:

Here the gravity is neglected and the field velocities is time independent, so we can use a simplify equation to Navier-Stokes.

`(DV)/(Dt) = -(1)/(\rho) \\abla p`

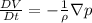
V: Field Flow

ρ: Density

p: pressure

Before finding the pressure, let's define the components of the field vector.

`V= 2xyi - y^(2)j`

`u=2xy`
`v = y^(2)`

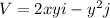
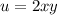
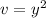
Now, the x component pressure gradient will be:

`u(\partial u)/(\partial x) + v(\partial u)/(\partial y) = -(1)/(\rho) (\partial p)/(\partiala x)`

`4xy^(2)-2xy^(2) = -(1)/(\rho) (\partial p)/(\partial x)`

`(\partial p)/(\partial x) = -\rho 2xy^(2)`

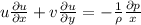
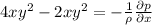
We can apply the same analyze to find the y component of the pressure gradient. We just need to take the partial derivative from v.

`u(\partial v)/(\partial x) + v(\partial v)/(\partial y) = -(1)/(\rho) (\partial p)/(\partial y)`

`0-2y^(3) = -(1)/(\rho) (\partial p)/(\partial x)`

`(\partial p)/(\partial y) = \rho 2y^(3)`

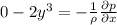
I hope it helps you! :)