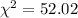Answer: C)
Explanation:
Given : It is desired to determine if the population standard deviation exceeds 20 minutes.
i.e.
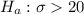
Here, we perform chi-square test.
Sample size : n= 51
Sample standard deviation : s= 20.40
The test statistic for chi-square test is given by :-
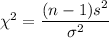
, where n= sample size
s= sample standard deviation.
 = Population standard deviation.
= Population standard deviation.
Substitute the values , we get
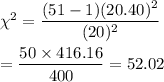
Hence, the test statistic for this test of hypothesis=
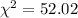
Thus , the correct answer is C)