Question

Determine the radial acceleration of the ultracentrifuge using calculations

Answer 1

When something moves on a round track, the guidance of the something's velocity must continually switch. A switching velocity means that there must be an acceleration. This acceleration is horizontal to the guidance of the velocity. This is said as “the radial acceleration”, or “centripetal acceleration” ("centripetal" means "center searching"). The “radial acceleration” is equal to “the square of the velocity”, divided by “the radius of the circular path of the object”. The unit of the “centripetal acceleration” is m/s².

`\text { Centripetal acceleration }=\frac{\text {velocity}^(2)}{\text {radius of motion}}`

`\mathrm{a}_{\mathrm{rad}}=(V^(2))/(r)`

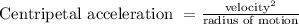
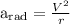
where,

`\text { and }=\text { radial, or centripetal, acceleration }(\mathrm{m} / \mathrm{s} ^2)`

"v" = "velocity" (m/s) and "r" = "radius of motion of the object" (m)