Answer:
The rate is needed is 1.037%.
Explanation:
Given : Suppose $1,500 is compounded weekly for 46 years. If no other deposits are made.
To find : What rate is needed for the balance to triple in that time?
Solution :
Applying compound interest formula,
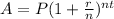
Where, P is the principal
A is the amount
The balance to triple in that time i.e. A=3P
r is the rate
t is the time t=46 years
Compounded weekly so n=52
Substitute the value in the formula,

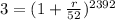
Taking log both side,
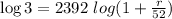
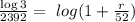

Taking exponential both side,
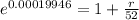

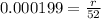
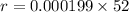

Into percentage,
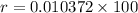

Therefore, the rate is needed is 1.037%.