Answer:
The horizontal component of the minimum force is 144.24 N.
Step-by-step explanation:
Given that,
Loaded = 23.90 kg
Height = 0.370 R
Where, R=wheel's radius
We need to calculate the acceleration
Using formula of acceleration
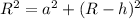

Put the value into the formula
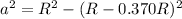
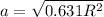
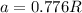
We need to calculate the horizontal component of the minimum force
Using moment about center of point of contact
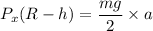
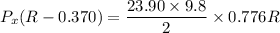
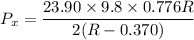
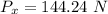
Hence, The horizontal component of the minimum force is 144.24 N.