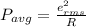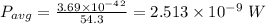Question

A sinusoidally oscillating current ????(????) with an amplitude of 5.55 A and a frequency of 359 cycles per second is carried by a long, straight wire. A rectangular loop of copper wire with dimensions ????=72.2 cm by c=32.5 cm is located ????=80.2 cm from the straight wire, and is coplanar with it. Calculate the average power Pavg dissipated by the loop if its resistance is 54.3 Ω.

Answer 1

`P_(avg) = 2.513* 10^(- 9)\ W`

Solution:

As per the question:

Current, I(t) = 5.55 A

Frequency, f = 359 Hz

B = 72.2 cm

c = 32.5 cm

a = 80.2 cm

Resistance, R = 54.3
`\Omega`

Now,

Th magnetic flux of the loop is given by:

`\phi = (\mu_(o)cI)/(2\pi )ln((a + b)/(a))`

Now,

I(t) =
`I_(o)sin\omega t`

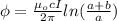
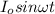
Now, the magnitude of the induced emf is given by:

`e = (d\phi)/(dt)`

`e = (d)/(dt)((\mu_(o)c* I_(o)sin\omega t)/(2\pi )ln((a + b)/(a)))`

`e = (\mu_(o)c* I_(o).ln((a + b)/(a)))(d)/(dt)(sin\omega t)/(2\pi )`

`e = (\omega \mu_(o)c* I_(o)cos\omega t.ln((a + b)/(a))))/(2\pi )`

`\omega = 2\pi f`

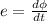
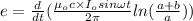
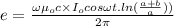
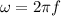
The rms value of the induced emf is given by:

`e_(rms) = ((2\pi f\mu_(o)I_(o)c)/(2\pi).ln((a + b)/(a)))/(√(2))`

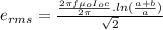
Substituting appropriate values in the above eqn:

`e_(rms) = ((2\pi * 359* 4\pi * 10^(- 7)* 0.325* 5.55)/(2\pi).ln((0.802 + 0.722)/(0.802)))/(√(2))`

`e_(rms) = 3.69* 10^(- 4)\ V`

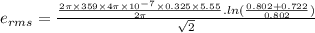
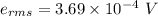
Now,

To calculate average power:

`P_(avg) = (e_(rms)^(2))/(R)`

`P_(avg) = (3.69* 10^(- 4)^(2))/(54.3) = 2.513* 10^(- 9)\ W`