Question

The combined statement of the first and second laws for the change in enthalpy of unary single-phase system may be written: dH' = TdS' +V'dP +udn use this result to write an expression for the change in enthalpy of a two-phase (alpha + beta) system. If the entropy, pressure, and total number of moles are constrained to be constant, then the criterion for equilibrium is that the enthalpy is a minimum. Paraphrase the strategy used to deduce the conditions for equilibrium in an isolated system to derive them for a system constrained to constant S', P and n. What happens to the condition for mechanical equilibrium?

Answer 1

Step-by-step explanation:

`dH{}'= TdS{}'+V{}'dP+\mu dn`

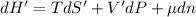
For ∝ phase system,

`dH{}'^(\alpha )= T^(\alpha )dS{}'^(\alpha )+V{}'^(\alpha )dP^(\alpha )+\mu^(\alpha ) dn^(\alpha )`

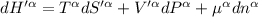
For β phase system,

`dH{}'^(\beta )= T^(\beta)dS{}'^(\beta )+V{}'^(\beta)dP^(\beta)+\mu^(\beta) dn^(\beta)`

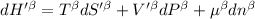
Now we know that the total enthalpy is the sum of the enthalpy in the alpha and beta phases.

∴
`H{}'_(sys)=H{}'^(\alpha )+H{}'^(\beta)`

`dH{}'_(sys)=dH{}'^(\alpha )+dH{}'^(\beta)`

`dH{}'_(sys)=\left (T^(\alpha )dS{}'^(\alpha )+V{}'^(\alpha )dP^(\alpha )+\mu^(\alpha ) dn^(\alpha )  \right )+\left (T^(\beta)dS{}'^(\beta )+V{}'^(\beta)dP^(\beta)+\mu^(\beta) dn^(\beta)  \right )`

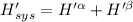
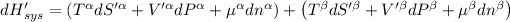
Now P, S an n are constants.

Then for isolated system, we get,

`dU{}'_(sys)=d\left ( U{}'^(\alpha) + U{}'^(\beta )\right ) =0`

`d U{}'^(\alpha)= - dU{}'^(\beta )`

`dV{}'_(sys)=d\left ( V{}'^(\alpha) + V{}'^(\beta )\right ) =0`

`d V{}'^(\alpha)= - dV{}'^(\beta )`

`dn{}'_(sys)=d\left ( n{}'^(\alpha) + n{}'^(\beta )\right ) =0`

`d n{}'^(\alpha)= - dn{}'^(\beta )`

`dP{}'_(sys)=d\left ( P{}'^(\alpha) + P{}'^(\beta )\right ) =0`

`dS{}'_(sys)=d\left ( S{}'^(\alpha) + S{}'^(\beta )\right ) =0`

`dS{}'^(\alpha)= - dS{}'^(\beta )`

`dH{}'_(sys) = dS{}'^(\alpha )\left ( T^(\alpha) -T^(\beta ) \right )+ dP{}'^(\alpha )\left ( V^(\alpha) -V^(\beta ) \right )+dn{}'^(\alpha )\left ( T^(\alpha) -T^(\beta ) \right )`

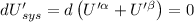
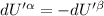
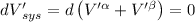
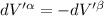
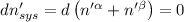
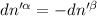
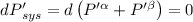
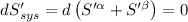
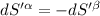
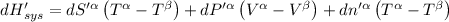
For equilibrium,

`dS{}'_(sys,iso)=0`

Then
`T^(\alpha )=T^(\beta )` ----- for thermal equilibrium

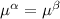`\mu ^(\alpha )=\mu ^(\beta )`----- for chemical equilibrium

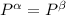`P^(\alpha )=P^(\beta )` ----- for mechanical equilibrium

The above conditions are valid for one component two phase system.