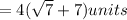Question

The area of a square equals the square of a length of the side of the square. The perimeter of a square equals the sum of the lengths of all four sides. The sum of the areas of two squares is 65, while the difference in their areas is 33. Find the sum of their perimeters.

Answer 1

Explanation:

Let us take side of first square be a

and other square side be L

It is given area of first square is equal to length of other

i.e.
`a^2=L`

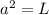
also

Sum of area of two square is 65

`L^2+a^2=65`

i.e.

`a^4+a^2=65----1`

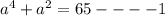
also Difference of area of two square is

`L^2-a^2=33`

`a^2-a^2=33-----2`

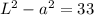
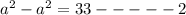
adding 1 and 2 we get

`2a^4=98`

`a^4=49`

`a^2=7`

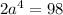
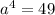
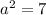
i.e.
`L=7`

and
`a=√(7)`

Perimeter of first Square

`P_1=4a=4√(7)`

`P_2=4 L=4* 7`

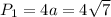
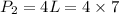
Sum of Perimeter

`=4(√(7)+7) units`

Answer 2

44

Explanation:

Let the side length of the larger square be x and the side length of the smaller square be y. We are told x^2 + y^2 = 65 and x^2 - y^2 = 33. Adding these two equations gives 2x^2 = 98, so x^2 = 49. Since x must be positive, we have x=7. Substituting this into either equation above gives us y^2 = 16. Since y must be positive, we have y=4. The perimeter of the larger square is 4x and that of the smaller square is 4y, so the sum of their perimeters is 4x+4y = 4(x+y) = \boxed{44}