Question

Flying with the wind, a small plane flew 340 mi in 2 h. Flying against the wind, the plane could fly only 310 mi in the same amount of time. Find the rate of the plane in calm air and the rate of the wind.

Answer 1

Rate of the plane in calm air is 162.6 miles per hour and the rate of the wind is 7.5 miles per hour

Solution:

Given that

Flying with the wind, a small plane flew 340 mi in 2 hrs .

Flying against the wind, the plane could fly only 310 mi in 2hrs

Need to find the rate of the plane in calm air and the rate of the wind.

As Flying with the wind, a small plane flew 340 mi in 2 hrs ,

So speed(rate) of the plane when Flying with the wind =
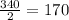`(340)/(2) = 170` miles per hour

As flying against the wind, the plane could fly only 310 mi in 2hrs ,

So speed (rate) of the plane when Flying against the wind =
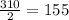`(310)/(2)=155`miles per hour

Let assume speed(rate) of the pane in calm air = x miles per hour

And speed(rate) of the wind = y miles

As speed ( rate ) while Flying with the wind = speed(rate) of the pane in calm air + speed(rate) of the wind

=> 170 = x + y

=> x + y = 170 ------(1)

As speed ( rate ) while Flying against the wind = speed(rate) of the pane in calm air - speed(rate) of the wind

=> 155 = x – y

=> x – y = 155 ------(2)

Adding (1) and (2) , we get

(x + y) + ( x - y) = 170 + 155

=> 2x = 325

=>
`x = (325)/(2)=162.5`

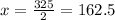
Substituting value of x in equation 1 , we get

162.5 + y = 170

=> y = 170 – 162.5 = 7.5

Hence rate of the plane in calm air = x = 162.6 miles per hour and the rate of the wind = y = 7.5 miles per hour.