Question

The daily revenue from the sale of fried dough at a local street vendor in Boston is known to be normally distributed with a known standard deviation of $120. The revenue on each of the last 25 days is noted, and the average is computed as $550. Construct a 95% confidence interval for the population mean of the sale of fried dough by this vendor.

Answer 1

$502.96 to $597.04

Explanation:

Mean sample revenue (μ) = $550

Standard deviation (σ) = $120

Sample size (n) = 25 days

The lower and upper bound for a 95% confidence interval are given by:

`U=\mu +1.960*(\sigma)/(√(n))\\L=\mu -1.960*(\sigma)/(√(n))`

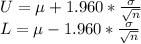
Applying the given data:

`U=550 +1.960*(120)/(√(25))\\U= \$597.04\\L=550 -1.960*(120)/(√(25))\\L= \$502.96`

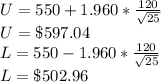
The 95% confidence interval is $502.96 to $597.04.