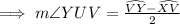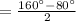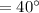Question

If arc XV = 80° and arc YX = 120°, what is the measure of ?YUV?

Answer 1

The measure of angle YUV is 40°

Explanation:

Consider the diagram of this question is attached below,

Where, Tangent line UV and secant XY intersect outside the circle at U,

Since,

`\widehat{XV}+\widehat{XY}+\widehat{VY}=360^(\circ)`

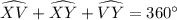
We have,

`\widehat{XV}=80^(\circ), \widehat{XY}=120^(\circ)`

`\implies 80^(\circ)+120^(\circ)+\widehat{VY}=360^(\circ)`

`200^(\circ)+\widehat{VY}=360^(\circ)`

`\widehat{VY}=360^(\circ)-200^(\circ)=160^(\circ)`

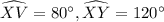
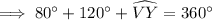
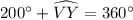
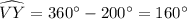
Since, the measure of intercepted angle outside the circle is half of the difference of measure of intercepted arcs,

`\implies m\angle YUV = \frac{\widehat{VY}-\widehat{XV}}{2}`

`=(160^(\circ)-80^(\circ))/(2)`

`=(80^(\circ))/(2)`

`=40^(\circ)`