Answer:
(221.39, 300.61) and (255.2223, 266.7777)
Explanation:
Given that X, the lengths of pregnancies in a small rural village are normally distributed with a mean of 261 days and a standard deviation of 17 days
Middle 98% would lie on either side of the mean with probability ±2.33 in the std normal distribution on either side of 0
Corresponding we have x scores as
Between
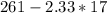 and
and

i.e. in the interval = (221.39, 300.61)
If sample size = 47, then std error of sample would be
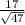
So 98% of pregnancies would lie between
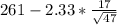 and
and

= (255.2223, 266.7777)