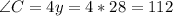Answer:
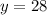
Explanation:
This is an isosceles triangle, which are a type of triangles that have a pair of equal sides. Having at least one pair of equal sides allows isosceles triangles to have well-known features. For example, the pair of angles adjacent to the base have the same value because they oppose equal sides within the same triangle.
So, in this case:
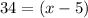
Solving for x:
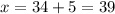
Thus:
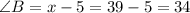
So, since the sum of the interior angles of a triangle is equal to 180:

Solving for y:
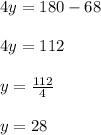
And: