Question

The proportion of junior executives leaving large manufacturing companies within three years is to be estimated within 3 percent. The 0.95 degree of confidence is to be used. A study conducted several years ago revealed that the percent of junior executives leaving within three years was 21. To update this study, the files of how many junior executives should be studied?

Also - for a question like this, how do we know what formula to use?

Answer 1

Answer: 709

Explanation:

The formulas we use to find the required sample size :-

1.
`n=((z^*\cdot \sigma)/(E))^2`

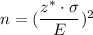
, where
`\sigma` = population standard deviation,

E = Margin of error .

z* = Critical value

2.
`n=p(1-p)((z^*)/(E))^2` , where p= prior estimate of population proportion.

3. If prior estimate of population proportion is unavailable , then we take p= 0.5 and the formula becomes

`n=0.25((z^*)/(E))^2`

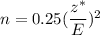
Given : Margin of error : E= 3% =0.03

Critical value for 95% confidence interval = z*= 1.96

A study conducted several years ago revealed that the percent of junior executives leaving within three years was 21%.

i.e. p=0.21

Then by formula 2., the required sample size will be :

`n=0.21(1-0.21)((1.96)/(0.03))^2`

`n=0.21(0.79)(65.3333)^2`

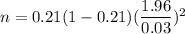
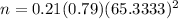
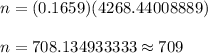`n=(0.1659)(4268.44008889)\\\\ n=708.134933333\approx709` [Round to the next integer.]

Hence, the required sample size of junior executives should be studied = 709