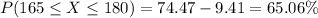Question

The weight of male students at a certain university is normally distributed with a mean of 175 pounds with a standard deviation of 7.6 pounds. Find the probabilities. 1. A male student weighs at most 186 pounds. 2. A male student weighs at least 160 pounds. 3. A male student weighs between 165 and 180 pounds.

Answer 1

1.) 92.61%

2.) 97.58%

3.) 65.06%

Explanation:

Mean populational weight (X) = 175 pounds

Standard deviation (σ) = 7.6 pounds

The z-score for any given student weight, X, is defined by:

`z=(X- \mu)/(\sigma)`

The z-score can be converted to a percentile of the normal distribution through a z-score table.

1.

The z-score for X=186 pounds is:

`z=(186- 175)/(7.6)\\z=1.447`

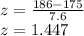
A z-score of 1.447 corresponds to the 92.61-th percentile.

Therefore, the probability that a male student weighs at most 186 pounds is:

`P(X\leq 186) = 92.61\%`

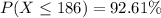
2.

The z-score for X=160 pounds is:

`z=(160- 175)/(7.6)\\z=-1.974`

A z-score of 1.447 corresponds to the 2.42-th percentile.

Therefore, the probability that a male student weighs at least 160 pounds is:

`P(X\geq 160) = 100 - 2.42=97.58\%`

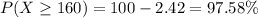
3.

The z-score for X=165 pounds is:

`z=(165- 175)/(7.6)\\z=-1.316`

A z-score of -1.316 corresponds to the 9.41-th percentile.

The z-score for X=180 pounds is:

`z=(180- 175)/(7.6)\\z=0.658`

A z-score of 0.658 corresponds to the 74.47-th percentile.

Therefore, the probability that a male student weighs between 165 and 180 pounds is:

`P(165\leq X\leq 180) = 74.47-9.41=65.06\%`