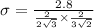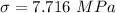Answer:
Stress is 7.716 MPa
Solution:
As per the question:
Magnitude of the resolved shear stress,
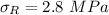
No. of atoms in Body Centered Cubic Crystal, n = 2
Now,
Shear stress is given by:

where
 = angle between slip plane and the tensile axis
= angle between slip plane and the tensile axis
 = angle between tensile axis and the slip direction, i.e., [1 2 1] and
= angle between tensile axis and the slip direction, i.e., [1 2 1] and
![[\bar{1}\ 1\ 1]](https://img.qammunity.org/2020/formulas/engineering/college/c5nfk0uxsimzkw3gbgukbd5bjk3k1jty4b.png)
Direction of applied force: [1 2 1]
Plane: [1 0 1]
Direction:
![[\bar{1}\ 1\ 1]](https://img.qammunity.org/2020/formulas/engineering/college/c5nfk0uxsimzkw3gbgukbd5bjk3k1jty4b.png)
Also, we know that:
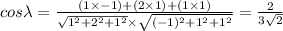
Now,
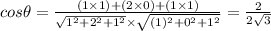
Now,
Stress,