Answer:
The equation of the regression line is:
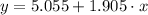
Explanation:
We have the following data:
![\begin{array}ccccccccccProductivity&23&25&28&21&21&25&26&30&34&36\\Dexterity&49&53&59&42&47&53&55&63&67&75\end{array}]()
We can use the Least Squares Regression to find the line of best fit for a set of paired data.
To find the line of best fit for n points:
Step 1: For each (x,y) point calculate
 and xy.
and xy.
Step 2: Sum all x, y,
 and xy, which gives us Σx, Σy,
and xy, which gives us Σx, Σy,
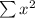 and Σxy.
and Σxy.
Step 3: Calculate Slope b:
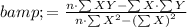
where n is the number of points.
Step 4: Calculate Intercept a:
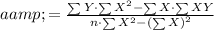
Step 5: Assemble the equation of a line
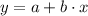
Following the above steps we get:
Step 1: Find
 and xy as it was done in the table
and xy as it was done in the table
Step 2: Find the sum of every column:
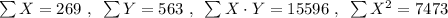
Step 3: Use the following equations to find a and b:
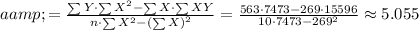
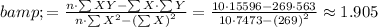
Step 4: Assemble the equation of a line
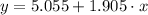
The graph of the regression line is: