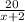Question

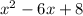
Divide. If there is a remainder, express it in the form r x + 2 . ( x 3 − 4 x 2 − 4 x + 36 ) ÷ ( x + 2 )

Answer 1

Quotient=
`x^2-6x+8`

Remainder=
`(20)/(x+2)`

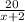
Explanation:

We are given that an expression

`(x^3-4x^2-4x+36)/(x+2)`

We have to divide and express remainder in the form rx+2.

We have

Divisor: The polynomial which divides the dividend polynomial.

Dividend: The polynomial which is divided by the divisor.

Dividend=
`x^3-4x^2-4x+36`

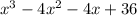
Divisor=
`x+2`

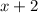
Quotient: The polynomial which is obtained when the divisor divides the dividend.

Remainder: The polynomial which remains when the divisor divides the dividend.

Quotient=
`x^2-6x+8`

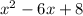
Remainder=
`(20)/(x+2)`