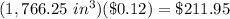Question

Goran's company makes solid balls out of scrap metal for various industrial uses. For one project, he must make aluminum balls that have a radius of 7.5 . If aluminum costs $0.12 per in³, how much will the aluminum cost to make one ball?

Use 3.14 for π , and do not round your answer.

Answer 1

Answer:
`\$211.95`

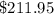
Explanation:

For this exercise it is important to remember the following formula, which is used to calculate the volume of a sphere:

`V=(4)/(3)\pi r^3`

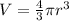
Where "r" is the radius of the sphere.

You know that the radius of one of those aluminum balls is:

`r=7.5\ in`

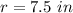
Then, subsituting this value into the formula and using
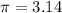`\pi =3.14`, you get that its volume is:

`V=(4)/(3)(3.14) (7.5\ in)^3\\\\V=1,766.25\ in^3`

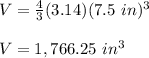
Since
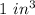`1\ in^3` of aluminum costs $0.12, you need to multiply the volume calculated by $0.12 in order to find how much the aluminum will cost to make one ball. This is:

`(1,766.25\ in^3)(\$0.12)=\$211.95`