Question

Visitors to a carnival can buy an unlimited-ride pass for $50 or an entrance-only pass for $20. In one day, 282 passes were sold for a total of $10,680. How many unlimited-ride passes were sold?

Answer 1

Number of Unlimited passes sold were 168.

Explanation:

Let Number of Unlimited passes sold be x

and Number of entrance-only passes sold be y.

Total number of passes sold =282

Hence,

`x+y=282 \ \ \ \ equation \ 1`

Also

Cost for unlimited-ride pass = $50

Cost for entrance-only pass = $20

Total Money for one day = $10,680

Hence,

`\$50x+\$20y=\$10,680\\`

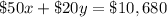
Dividing by 10 on both side we get;

`5x+2y=1068 \ \ \ \ equation \ 2`

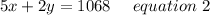
Now multiplying equation 1 by 2 we get;

`2x+2y=584 \ \ \ \ equation \ 3`

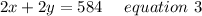
Now Subtracting equation 3 from equation 2 we get;

`(5x+2y=1068)-(2x+2y=584)\\3x=504\\x=(504)/(3)= 168`

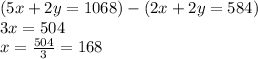
x= 168

x+y = 282

168+y =282

y=282-168

y= 114

Hence, Number of Unlimited passes sold are 168 and Number of entrance-only pass sold is 114.