Question

What is the maximum value of the objective function, P, with the given constraints? P=15x+20y

x+y≤15

2x+y≤25

x≥0

y≥0

Answers:

225 250 300 500

Answer 1

Option C.

Explanation:

The given objective function is

`P=15x+20y`

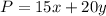
Subject to constraints.

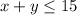`x+y\leq 15` .... (1)

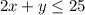`2x+y\leq 25` .... (2)

`x\ge 0,y\ge 0`

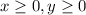
The related equations of given inequalities are

`x+y=15`

`2x+y=25`

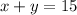
Table of values:

For inequality (1).

x y

0 15

15 0

For inequality (2).

x y

0 25

12.5 0

Plot these ordered pairs and draw the related lines.

Check both inequalities by (0,0).

`(0)+(0)\leq 15\Rightarrow 0\leq 15` True

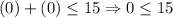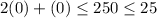`2(0)+(0)\leq 25\Rightarow 0\leq 25` True

In means (0,0) included in shaded region of both inequalities.
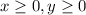`x\ge 0,y\ge 0` means first quadrant.

From the below graph it is clear that the vertices of feasible region are (0,0), (0,15), (10,5) and (12.5,0).

Point P=15x+20y

(0,0) P=15(0)+20(0)=0

(0,15) P=15(0)+20(15)=300

(10,5) P=15(10)+20(5)=250

(12.5,0) P=187.5+20(0)=0

The maximum value of objective function is 300 at x=0 and y=15.

Therefore, the correct option is C.