Answer:
Choose the first alternative
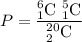
Explanation:
Probabilities
The requested probability can be computed as the ratio between the number of ways to choose two sophomores in alternate positions
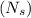 and the total number of possible choices
and the total number of possible choices
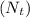 , i.e.
, i.e.
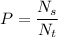
There are 6 sophomores and 14 freshmen to choose from each separate set. There are 20 students in total
We'll assume the positions of the selections are NOT significative, i.e. student A/student B is the same as student B/student A.
To choose 2 sophomores out of the 6 available, the first position has 6 elements to choose from, the second has now only 5
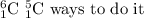
The total number of possible choices is
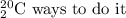
The probability is then
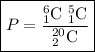
Choose the first alternative