Question

Flower grow rapidly.A flower is 60 inches tall.Tomorrow it will be 71 inches tall.The next day it will be 82 inches tall,and on the next day it will be 93 inches tall.Write a rule to represent the height of the flower as an arithmetic sequence.How tall will the plant be in 12 days

Answer 1

`\text{Height of flower on }n^(th)\text{ day} = a_n = a_1+(n-1)d`

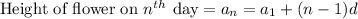
Height of flowers in 12 days = 181 inches

Explanation:

We are given the following information in the question:

A flower is 60 inches tall. Next day it is 71 inches tall. The next day it is 82 inches tall. The next day it is 93 inches tall.

If it grows in the same manner we have to write a rule to approximate the height of the flower.

Height of flower:

`60, 71, 82, 93,...`

The height of flower forms an arithmetic progression of the form:

`a_1,a_2,a_3,...\\a, a+d, a+2d,...\\\text{where a is the first term and d is the common difference.}`

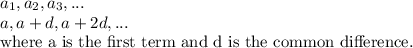
Comparing we get:

`a_1 = 60\\d = 71-60 = 11`

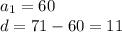
Thus, the height of flower on
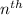`n^(th)` day will be given by the
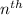`n^(th)` term of the arithmetic progression, that is given by:

`\text{Height of flower on }n^(th)\text{ day} = a_n = a_1+(n-1)d`

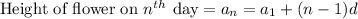
Height of flowers in 12 days =

`a_(12) = a_1 + (n-1)d = 60 + (12-1)11 = 60 + (11)11 = 181\text{ inches}`