Question

When bonding teeth, orthodontists must maintain a dry field. A new bonding adhesive (called Smartbond) has been developed to eliminate the necessity of a dry field. However there is concern that the new bonding adhesive is not as strong as the current standard, a composite adhesive (Trends in Biomaterials & Artificial Organs, Jan. 2003). Tests on a sample of 10 extracted teeth bonded with the new adhesive resulted in a mean breaking strength (after 24 hours) of x bar = 5.07 Mpa and a standard deviation of s= .46 Mpa. Orthodontists want to know if the mean breaking strength of the new bonding adhesive is less than 5.70 Mpa, the mean breaking strength of the composite adhesive.

a. Set up the null and alternative hypotheses for the test.b. Find the rejection region for the test using significance level=.01.c. Compute the test statistic.d. Give the appropriate conclusion for the test.e. What conditions are required for the test results to be valid?

Answer 1

a) Null hypothesis:
`\mu \geq 5.7`

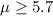
Alternative hypothesis :
`\mu<5.7`

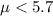
b)
`t_(crit)=-2.82`

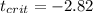
The rejection regin would be (-infinity;-2.82)

c)
`t=(5.07-5.7)/((0.46)/(√(10)))=-4.33`

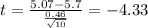
d) If we compare the p value and the significance level for example
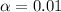`\alpha=0.01` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, so we can conclude that the mean breaking strength of the new bonding adhesive is significantly less than 5.7Mpa at 1% of significance.

e) See below the explanation.

Explanation:

Data given and notation

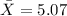`\bar X=5.07` represent the mean breaking strength value for the sample

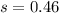`s=0.46` represent the sample standard deviation

`n=10` sample size

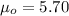`\mu_o =5.70` represent the value that we want to test

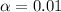`\alpha=0.01` represent the significance level for the hypothesis test.

t would represent the statistic (variable of interest)

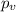`p_v` represent the p value for the test (variable of interest)

a) State the null and alternative hypotheses.

Is a one tailed left test.

What are H0 and Ha for this study?

Null hypothesis:
`\mu \geq 5.7`

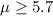
Alternative hypothesis :
`\mu<5.7`

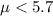
b) Find the rejection region for the test using significance level=.01

First we need to find the degrees of freedom on this case:

`df=n-1=10-1=9`

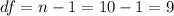
In order to find the critical value we need to find a value on the normal standard distribution such that:

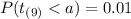`P(t_((9))<a)=0.01` where 0.01 represent the significance level selected.

And this value is
`t_(crit)=-2.82`

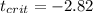
The rejection regin would be (-infinity;-2.82)

c) Compute the test statistic

The statistic for this case is given by:

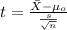`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

t-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

Calculate the statistic

We can replace in formula (1) the info given like this:

`t=(5.07-5.7)/((0.46)/(√(10)))=-4.33`

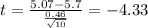
d) Give the appropriate conclusion for the test

Since is a one side left tailed test the p value would be:

`p_v =P(t_((9))<-4.33)=0.00095`

Conclusion

If we compare the p value and the significance level for example
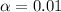`\alpha=0.01` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, so we can conclude that the mean breaking strength of the new bonding adhesive is significantly less than 5.7Mpa at 1% of significance.

e) What conditions are required for the test results to be valid?

The first assumption made regarding t-tests concerns the scale of measurement. The assumption for a t-test is that the scale of measurement applied to the data collected follows a continuous or ordinal scale (Assumed)

The second assumption made is that of a simple random sample, that the data is collected from a representative, randomly selected portion of the total population. (Assumed)

The third assumption is the data comes from a normal distribution, bell-shaped distribution curve. (Assumed)

The fourth assumption is a reasonably large sample size is used. (For this case we can asume that a sample size of 10 is enough to conduct a t test)