Question

How many solutions are there to the system of equations?

StartLayout enlarged left-brace 1st row 4 x minus 5 y = 5 2nd row negative 0.08 x + 0.10 y = 0.10 EndLayout

Answer 1

answer: A

(no solutions)

your welcome

Answer 2

Answer: The system of equations has NO SOLUTION.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the following system of equations:

`\left \{ {{4x-5y=5} \atop {-0.08x+0.10y=0.10}} \right.`

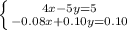
Write the first equation and solve for "y" in order to express it in Slope-Intercept form:

`4x-5y=5\\\\-5y=-4x+5\\\\y=(-4x)/(-5)+(5)/(-5)\\\\y=0.8x-1`

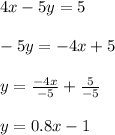
You can identify that:

`m=0.8\\b=-1`

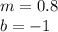
Apply the same procedure with the second equation. Then:

`-0.08x+0.10y=0.10\\\\0.10y=0.08x+0.10\\\\y=(0.08x)/(0.10) +(0.10)/(0.10)\\\\y=0.8x+1`

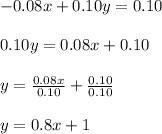
You can identify that:

`m=0.8\\b=1`

The slopes of both lines are equal, therefore the lines are parallel and the system has NO SOLUTION.