Question

Given the functionLaTeX: f(x)=\frac{x^2+7x+10}{x^2+9x+20}f ( x ) = x 2 + 7 x + 10 x 2 + 9 x + 20

Describe where the function has a vertical asymptote and how you found your answer. Remember that an asymptote is represented by an equation of a line and not just a single value.

Answer 1

The equation of Vertical asymptote is x+4=0

Explanation:

Figure shows vertical asymptote at x=4=0

Where redline is f(x) and blueline is vertical asymptote

Given the function is f(x) =
`(x^(2)+7x+10 )/(x^(2)+9x+20 )`

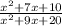
Step 1 : Simplifying denominator and numerator

For denominator

`x^(2)+9x+20=0`

`x^(2)+5x+4x+20=0`

`x(x+5)+4(x+5)=0`

`(x+4)(x+5)=0`

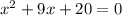
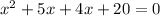
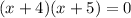
For numerator

`x^(2)+7x+10=0`

`x^(2)+5x+2x+10=0`

`(x+5)(x+2)=0`

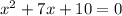
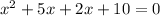
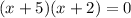
Step2 : Finding Vertical asymptote

After simplification of f(x)

f(x) =
`((x+5)(x+2))/((x+5)(x+4))`

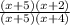
f(x) =
`((x+2))/((x+4))`

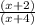
Here, Denominator will give Vertical asymptote.

Therefore, Vertical asymptote is x+4=0