Question

How do rented housing units differ from units occupied by their owners? Here are the distributions of the number of rooms for owner-occupied units and renter occupied units in San Jose, California.

--------------------------------------------------------------------------------

Rooms 1 2 3 4 5 6 7 8 9 10


Owned 0.003 0.002 0.023 0.102 0.209 0.223 0.201 0.149 0.053 0.035

Rented 0.008 0.027 0.287 0.371 0.155 0.090 0.043 0.013 0.003 0.003


Find the standard deviation for both distributions. The standard deviation provides a numerical measure of spread.

Owned ??

Rented ??

Answer 1

Standard deviation for owner-occupied units

2.9797

Standard deviation for renter-occupied units

3.1594

Explanation:

Let us find first the mean. This is the distribution expected value or expectancy.

Mean for owner-occupied units

0.003 + 2*0.002 + 3*0.023 + 4*0.102 + 5*0.209 + 6*0.223 + 7*0.201 + 8*0.149 + 9*0.053 + 10*0.035 = 6.293

To compute the variance for owner-occupied units, we add these values

`(1-6.293)^2+(2-6.293)^2+(3-6.293)^2+(4-6.293)^2+(5-6.293)^2`

`+(6-6.293)^2+(7-6.293)^2+(8-6.293)^2+(9-6.293)^2+(10-6.293)^2`

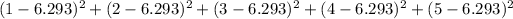
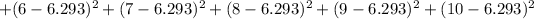
then divide by 10 and take the square root to get the standard deviation 2.9797

Mean for renter-occupied units

0.008 + 2*0.027 + 3*0.287 + 4*0.371 + 5*0.155 + 6*0.090 + 7*0.043 + 8*0.013 + 9*0.003 + 10*0.003 = 4.184

To compute the variance for renter-occupied units, we add these values

`(1-4.184)^2+(2-4.184)^2+(3-4.184)^2+(4-4.184)^2+(5-4.184)^2`

`+(6-4.184)^2+(7-4.184)^2+(8-4.184)^2+(9-4.184)^2+(10-4.184)^2`

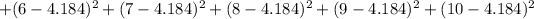
then divide by 10 and take the square root to get the standard deviation 4.184