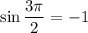Question

Use the unit circle to find the value of sin 3pi/2 and cos 3pi/2

Answer 1

The sine of 3π/2 using the unit circle is -1, and the cosine of 3π/2 is 0.

Step-by-step explanation:

Using the unit circle, the angle of 3π/2 radians corresponds to a position that is at the bottom of the circle, where the x-coordinate is 0 and the y-coordinate is -1. This means that:

• The cosine of 3π/2, which reflects the x-coordinate, is 0.
• The sine of 3π/2, which reflects the y-coordinate, is -1.

Sin(3π/2) = -1 because it's the ratio of the opposite side (Ay) to the hypotenuse (A) in a right triangle, and at this angle, the side is going straight down from the center of the circle.

Similarly, Cos(3π/2) = 0 as it's the ratio of the adjacent side (Ax) to the hypotenuse (A), and the side is at a zero distance from the x-axis because it coincides with the y-axis at this angle.

Answer 2

`\cos (3\pi)/(2)=0`

`\sin (3\pi)/(2)=-1`

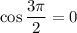
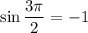
Step-by-step explanation:

First, determine the point on the unit circle which corresponds to angle
`(3\pi)/(2)` (that is 270° in degrees)

Start from point (1,0) - this point represents angle 0.

Point (0,1) represents angle
`(\pi)/(2)` (that is 90° in degrees) point (-1,0) represents angle
`\pi` (that is 180° in degrees) and point (0,-1) represents angle
`(3\pi)/(2).`

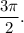
The first coordinate of this point is the value of cosine, then

`\cos (3\pi)/(2)=0`

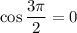
the second coordinate is the value of sine, then

`\sin (3\pi)/(2)=-1`