Question

Give the equation of a line in slope-intercept form with the following criteria:

Line passes through point (12,-5) that is perpendicular to y= (6/7)x+4

Answer 1

`y = - (7)/(6)x + 9`

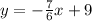
Explanation:

We need to find a straight line that is perpendicular to the line
`y = (6)/(7) x + 4`.

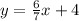So, the slope of the given straight line is
`(6)/(7)` {Since the equation is in slope-intercept form}

Now, the slope of the required straight line will be [tex]- \frac{7}{6}[/tex]

{Since, the product of slopes of two straight line that are perpendicular to each other is -1, and
`(6)/(7) * (- (7)/(6)) = - 1`}

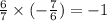Then the equation of the required straight line in slope-intercept form will be
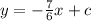`y = - (7)/(6) x + c` ............. (1) {Where c is any constant}

Now, point (12, -5) will satisfy the equation (1).

Hence,
`-5 = - (7)/(6)(12) + c`

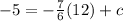
⇒ - 5 = - 14 + c

⇒ c = 9

Therefore, the complete equation of the required straight line is
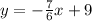`y = - (7)/(6)x + 9` (Answer)