In Problems 23–30, use the given zero to find the remaining zeros of each function 23. f(x) = x3 – 4x² + 4x – 16; zero: 2i

Question

asked Sep 7, 2020 223k views

1 Answer

Otheus · Answer 1 · 2020-09-13T03:09:51+0000

Answer:

x = 2i, x = -2i and x = 4 are the roots of given polynomial.

Explanation:

We are given the following expression in the question:

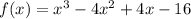
f(x) = x^3 - 4x^2+ 4x - 16

One of the zeroes of the above polynomial is 2i, that is :

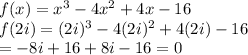
$f(x) = x^3 - 4x^2+ 4x - 16\\f(2i) = (2i)^3 - 4(2i)^2+ 4(2i) - 16\\= -8i+ 16+8i-16 = 0$

Thus, we can write

$(x-2i)\text{ is a factor of polynomial }x^3 - 4x^2 + 4x - 16$

Now, we check if -2i is a root of the given polynomial:

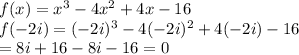
$f(x) = x^3 - 4x^2+ 4x - 16\\f(-2i) = (-2i)^3 - 4(-2i)^2+ 4(-2i) - 16\\= 8i+ 16-8i-16 = 0$

Thus, we can write

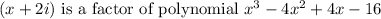
$(x+2i)\text{ is a factor of polynomial }x^3 - 4x^2 + 4x - 16$

Therefore,

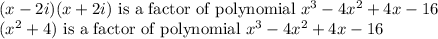
$(x-2i)(x+2i)\text{ is a factor of polynomial }x^3 - 4x^2 + 4x - 16\\(x^2 + 4)\text{ is a factor of polynomial }x^3 - 4x^2 + 4x - 16$

Dividing the given polynomial:

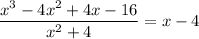
$\displaystyle(x^3 - 4x^2 + 4x - 16)/(x^2+4) = x -4$

Thus,

$(x-4)\text{ is a factor of polynomial }x^3 - 4x^2 + 4x - 16$

X = 4 is a root of the given polynomial.

$f(x) = x^3 - 4x^2+ 4x - 16\\f(4) = (4)^3 - 4(4)^2+ 4(4) - 16\\= 64-64+16-16 = 0$

Thus, 2i, -2i and 4 are the roots of given polynomial.