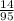Question

Kent has a bag with 8 blue marbles, 6 red marbles, and 6 green marbles in it. If he draws two marbles out of the bag one at a time without replacement, what is the probability that both marbles will be blue?

A. 1/10
B. 7/50
C. 14/95
D. 4/25
E. 16/95

Answer 1

C) The probability of drawing two blue marbles without replacement is
`(14)/(95)`

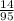
Explanation:

Total number of blue marbles = 8

Total marbles = Number of ( Blue + Red + Green) marbles

= 8+ 6 + 6 = 20 marbles

Now,Let E: Event of picking a blue marble

Also, we know that P (any Event E) =
`\frac{\textrm{Number of favorable outcomes}}{\textrm{ Total number of outcomes }}`

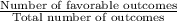
⇒ P( Picking first Blue marble) =
`\frac{\textrm{Number of blue marbles}}{\textrm{ Total number of marbles }}  = (8)/(20)`

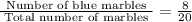
Now, again P( Picking second Blue marble) =
`\frac{\textrm{Number of blue marbles left}}{\textrm{ Total number of marbles left }}  = (7)/(19)`

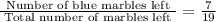
Again , P( Drawing two blue marbles without replacement)

= P( Picking first Blue marble) x P( Picking second Blue marble)

`= (8)/(20)  * (7)/(19)  = (14)/(95)`

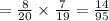
Hence, the probability of drawing two blue marbles without replacement from the bag is
`(14)/(95)`