Question

algebraically determine the values of h and k to correctly complete the identity stated below : 2 x cubed - 10x squared + 11x - 7 = (x-4)(2x squared)+ hx+3(+k)

Answer 1

The values for expression is h = - 2 and k = 5

Explanation:

Given algebraic expression can be written as :

2 x³ - 10 x² + 11 x - 7 = ( x - 4 ) × ( 2 x² + h x + 3 ) + k

Now opening the bracket

Or, 2 x³ - 10 x² + 11 x - 7 = x × ( 2 x² + h x + 3 ) - 4 × ( 2 x² + h x + 3 ) + k

Or, 2 x³ - 10 x² + 11 x - 7 = 2 x³ + h x² + 3 x - 2 x² - 4 h x - 12 +k

Or , 2 x³ - 10 x² + 11 x - 7 = 2 x³ + ( h - 2 ) x² + ( 3 - 4 h ) x - 12 + k

Now, equating the equation both sides

I.e - 10 = ( h - 2 )

Or , h - 2 = - 10

I.e , h = - 10 + 2

∴ h = - 2

Again , 11 = ( 3 - 4 h )

or, 11 = 3 - 4 h

or, 11 - 3 = - 4 h

or, 8 = - 4 h

∴ h =
`(-8)/(4)`

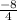
I.e h = - 2

Again

- 7 = - 12 + k

Or, k = - 7 + 12

∴ k = 5

Hence The values for expression is h = - 2 and k = 5 . Answer