Question

Line segment AB has a length of 3 units. It is translated 2 units to the right on a coordinate plane to obtain fine segment A'BWhat is the length of A'B'?

1 unit

2 units

3 units

5 units


i’ll mark you branlist!

Answer 1

Answer: The correct option is

(C) 3 units.

Step-by-step explanation: Given that a line segment AB has a length of 3 units. It is translated 2 units to the right on a coordinate plane to obtain fine segment A'B'.

We are to find the length of the line segment A'B'.

Let A(a, b) and B(c, d) be the endpoints of the line segment AB.

After translating 2 units to the right, the endpoints of the line segment A'B' are

`A(a,b)\Rightarrow A'(a+2,b+2),\\\\B(c,d)\Rightarrow B'(c+2,d+2).`

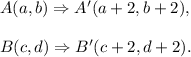
According to the given information, we have

`\textup{length of AB}=3\\\\\Rightarrow \textup{distance between A(a,b) and B(c,d)}=3\\\\\Rightarrow √((c-a)^2+(d-b)^2)=3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

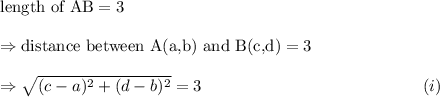
Therefore, the length of the line segment A'B' is

`A'B'=√((c+2-a-2)^2+(d+2-b-2)^2)=√((c-a)^2+(d-b)^2)=3~~~[\textup{Using (i)}].`

Thus, the required length of the line segment A'B' is 3 units.

Option (C) is CORRECT.