Question

you want to plot the collinear points A(-2,3), A'(x,y), and A"(3,7) on the same coordinate plane. Find the values of x and y.

Answer 1

`A'(2,(31)/(5))`

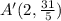
Explanation:

Remember that three points are collinears if they stay in the same line.

To find the line that pass through A(-2,3) and A''(3,7), we find first the slope of the line and then the y-intercept.

The slope of the line is

`m=(7-3)/(3-(-2))=(4)/(5)`

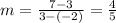
The y-intercept of the line is

`7=(4)/(5)*3+b\\b=(23)/(5)`

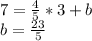
Then the equation of the line is

`y=(4)/(5)x+(23)/(5)`

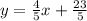
Since we want that the point A'(x,y) stay in the line, then we need to choose a value for x and replace in the equation found.

If we take x=2

`y=(4)/(5)*2+(23)/(5)=(31)/(5)`

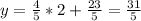
Then the points
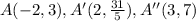`A(-2,3), A'(2, (31)/(5)), A''(3,7)` are collinear.