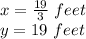Answer:
Explanation:
Derivatives and Optimization
We can find where a function f has points of maxima/minima by using the first derivative criteria, i.e. f'=0 and evaluate its critical points.
Let's say the rectangular area has dimensions x (height) and y (width) and we are going to split the width into thirds. The area of that rectangle is
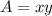
The perimeter of that rectangle is the length of the outside fence
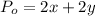
It costs $10 per feet, so the cost of the outside fence is
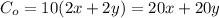
The dividers cost $20 per foot, and we have assumed we split the width, so each divider has a length of x feet. The cost of the internal dividers is
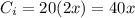
The total cost of the fencing is

We know there is a limit of $760 to spend for the fencing material, so

Reducing
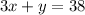
Solving for y
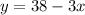
The area can be now expressed in terms of x alone
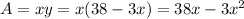
To find the critical point, and possible maxima/minima, we set A'=0
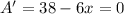
We find:
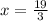
Since
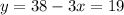
The second derivative is
A''=-6
This means the area is maximum at the critical point
The dimensions that maximize the area are: