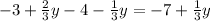Question

Can someone answer this in associative property and communitive property?

Answer 1

The required equivalent Expression is

`-3+(2)/(3)y -4 -(1)/(3)y =-7+(1)/(3)y`

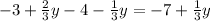
Explanation:

Associative property:

The associative property states that you can re-group numbers and you will get the same answer.

For Example:

A + (B + C) = (A + B) + C

Commutative property:

The commutative property states that you can move numbers around and still arrive at the same answer.

For Example:

A + B = B + A

Given:

`-3+(2)/(3)y -4 -(1)/(3)y`

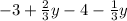
Using Commutative property and associative property we get

`-3+(2)/(3)y -4 -(1)/(3)y = -3 -4+(2)/(3)y -(1)/(3)y\\\\-3+(2)/(3)y -4 -(1)/(3)y = -7 +(2-1)/(3)y\\\\-3+(2)/(3)y -4 -(1)/(3)y =-7+(1)/(3)y`

Therefore the required equivalent Expression is

`-3+(2)/(3)y -4 -(1)/(3)y =-7+(1)/(3)y`