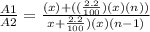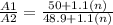Question

You have an amount of money in a savings account that earns simple interest at a fixed rate of 2.2% per year. From year to year, you do not deposit or withdraw money from the account. Write the ratio in simplest form of the amount in this account in the year n to the amount in the year n-1

Answer 1

`(50 + 1.1(n))/(48.9 + 1.1(n))`

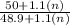
Explanation:

The simple interest is calculated only on initial amount deposited and so the interest per year is constant.

Let the initial amount be "x".

The interest for first n years is,

`((2.2)/(100))(x)(n)`

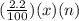
and so the final amount is

`A1 = (x) + (((2.2)/(100))(x)(n))`

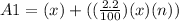
Similarly for n-1 years,

interest is =
`((2.2)/(100))(x)(n-1)`

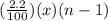
and amount is ,

A2 = x +
`((2.2)/(100))(x)(n-1)`

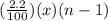
The required ratio is ,

`(A1)/(A2) = ((x) + (((2.2)/(100))(x)(n)))/(x + (2.2)/(100))(x)(n-1))`

`(A1)/(A2) = (50 + 1.1(n))/(48.9 + 1.1(n))`