Question

Use Identities to find the exact value.
24) cos(-75°)

Answer 1

`(1)/(4)`(
`√(6)` -
`√(2)`)

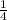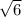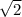Explanation:

Using the addition formula for cosine

cos(x - y) = cosxcosy + sinxsiny

and the exact values

sin45° = cos45° =
`(1)/(√(2) )`

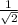
cos60° =
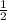`(1)/(2)`, sin60° =
`(√(3) )/(2)`

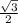
Note that

cos(- 75)° = cos(45 - 120)°, thus

cos(45 - 120)°

= cos45° cos120° + sin45° sin120°

= cos45° ( - cos60°) + sin45° sin60°

=
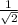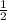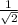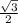
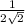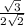
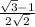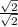
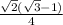
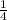`(1)/(√(2) )` × -
`(1)/(2)` +
`(1)/(√(2) )` ×
`(√(3) )/(2)`

= -
`(1)/(2√(2) )` +
`(√(3) )/(2√(2) )`

=
`(√(3)-1 )/(2√(2) )` ×
`(√(2) )/(√(2) )`

=
`(√(2)(√(3)-1)  )/(4)`

=
`(1)/(4)`(
`√(6)-√(2)`)