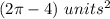Question

A square ABCD is inscribed in a circle. The square has a base edge of 2 inches.Find the area of the region restricted by the circle and outside of the square.

Answer 1

`(2 \pi-4)\ units^2`

Explanation:

see the attached figure to better understand the problem

we know that

The area of the region restricted by the circle and outside of the square is equal to the area of circle minus the area of square

step 1

Find the area of square

The area of square is

`A=b^(2)`

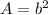
where

b is the length side of square

we have

`b=2\ in`

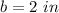
substitute

`A=2^(2)=4\ units^2`

step 2

Find the area of the circle

The area of the circle is equal to

`A=\pi r^(2)`

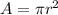
where

r is the radius of the circle

In this problem

The diameter of the circle is equal to the diagonal of the square

Find the diagonal of the square

Applying Pythagorean Theorem

`D=√(b^2+b^2)`

`b=2\ in`

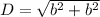
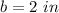
substitute

`D=√(2^2+2^2)`

`D=√(8)\ units`

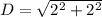
simplify

`D=2√(2)\ units`

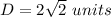
Find the radius of the circle

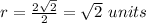`r=(2√(2))/(2)=√(2)\ units` ---> the radius is half the diameter

Find the area of the circle

`A=\pi r^(2)` ---->
`A=\pi(√(2))^(2)=2 \pi\ units^2`

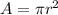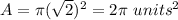
step 3

Find the area of the region restricted by the circle and outside of the square

Subtract the area of square from the area of the circle

`(2 \pi-4)\ units^2`